Electing a Single Winner When the Electorate is Divided in Multiple Ways

The third in a series of essays on the philosophy of democracy and its implications

This essay is part of a series on elections for single-winner offices, like the presidency. The question is how the philosophy of democracy should handle these elections, given the necessity to elect just one officeholder to represent all voters equally when voters have sharply varying preferences on who should represent them. The previous essays in this series have, first, examined this issue on the assumption that these varying preferences can be lined up along a single left-right dimension of partisanship and, second, observed that even after abandoning this assumption there can be instances in which one candidate is preferred by a majority of voters compared to each other candidate and thus this uniquely majority-preferred candidate is the one most deserving to win the election as most representative of the entire electorate for this necessarily singular office. In this third essay in the series, I consider the situation in which there is no uniquely majority-preferred candidate and discuss philosophically how best to determine which candidate should be the one to represent the entire electorate as the single officeholder, such as president or governor.

Let’s imagine that in the near future American electoral politics becomes contested along two distinct dimensions. The first and dominant dimension is the set of cultural issues that have become salient in recent years, as discussed in the work of political scientists like John Sides, Lynn Vavreck, and their coauthors. We could call this current left-right dimension “progressive versus populist” to convey the degree that social identity, including race, religion, and educational status, animates a voter’s position on this polarized spectrum of electoral competition. So-called “hot button” issues like abortion and guns are significant components of this basic blue-red divide.

As a result of these cultural issues becoming increasingly important, the traditional economic conflict between Democrats and Republicans has diminished in significance. Indeed, the Republican Party under Donald Trump’s leadership and its turn to MAGA populism has largely abandoned “balance the budget” fiscal conservatism in favor of large deficit spending. In its increasing appeal to lower-income voters, Trump’s MAGA-remade Republican Party has signaled a willingness to spend substantial sums on the kinds of social programs traditionally favored by Democrats while at the same time pursuing large-scale tax cuts. Given this realignment, neither of the two parties on the main blue-red dimension of electoral conflict are especially associated with fiscal discipline and deficit-cutting.

Let’s assume, then, that as America’s debt continues to escalate there opens up a second dimension of electoral competition as a growing cohort of politicians prioritize advocacy for fiscal responsibility and debt reduction while downplaying their position on the dominant blue-red cultural dimension of electoral conflict. We can envision these politicians as largely associated with the old non-MAGA version of the Republican Party. They want to distance themselves from what they see as MAGA populism’s fiscal irresponsibility, but they don’t consider themselves to be in the middle of the blue-red spectrum that defines the main dimension of electoral conflict. Rather, this group of politicians sees themselves as much more traditionalist than progressive, and thus much more red than blue when it comes to cultural issues.

Let’s further suppose that in a future election there is a three-way race between a Democrat, a MAGA Republican, and one of these “fiscal sanity” conservatives. If it helps to contemplate a concrete hypothetical example, suppose it’s a presidential election with Alexandria Ocasio-Cortez (AOC) as the Democratic nominee, JD Vance as Republican nominee, and Chris Sununu, the former New Hampshire governor, running as the nominee of a new Conservative Party. In this situation, the competition among these three candidates would play out in two dimensions: the first being dominant blue-red dimension between culturally progressive AOC and MAGA populist Vance, and the second between fiscally conservative Sununu and both AOC and Vance as fiscally liberal big spenders.

Because I want to make a general point that’s much broader than this single hypothetical (a point that could apply to congressional and other races and not just a presidential election), let’s make our illustrative example abstract with the three candidates being Blue, Red, and Gray. Blue is a progressive Democrat, Red is a MAGA populist, and Gray is a fiscal conservative—gray being an appropriate color to convey the warning that is this candidate’s main campaign message.

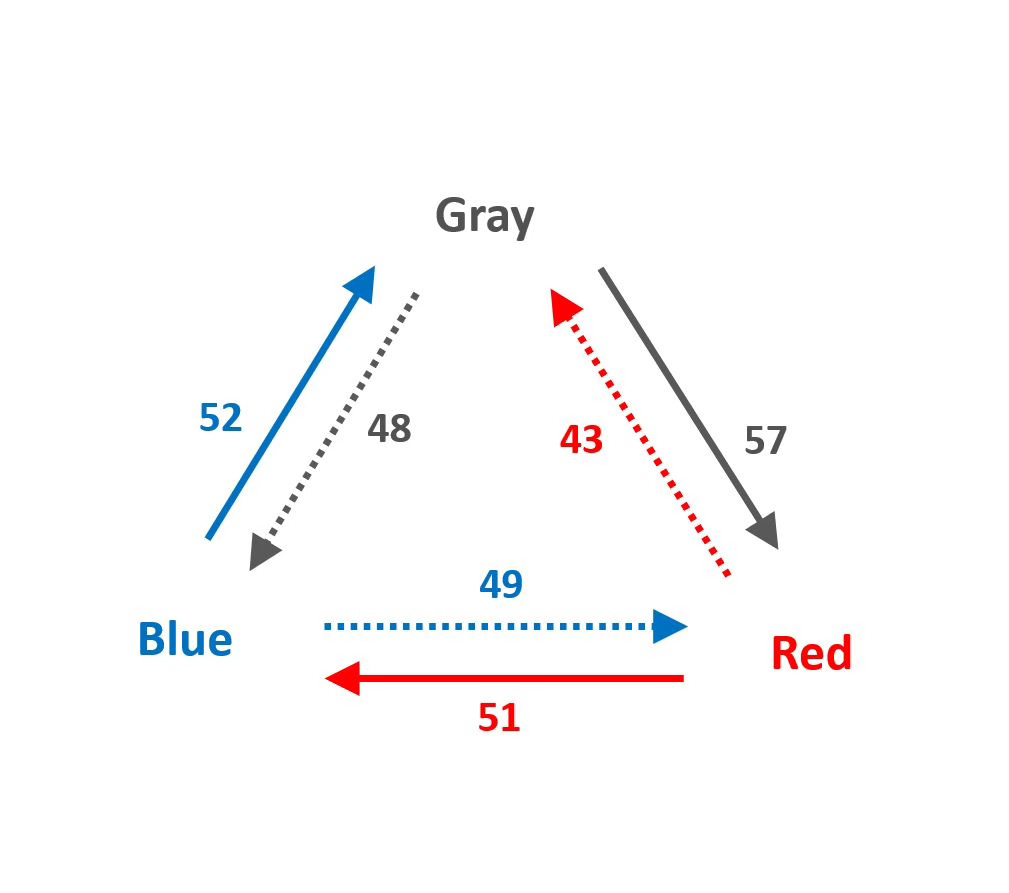
Let’s imagine that this three-candidate election was conducted using a Convergence Voting method, meaning that the ballots voters received asked them to indicate for each pair of candidates which of the two they preferred. Let’s assume these were the results:

Blue versus Red: 51% for Red, 49% for Blue

Blue versus Gray: 52% for Blue, 48% for Gray

Red versus Gray: 57% for Gray, 43% for Red

Each candidate is preferred by a majority of voters over one opponent but not the other.

In this situation, which candidate should win the election?

One possible way to answer this question is to take the average of each candidate’s margins of victory and defeat. This would be a measure of each candidate’s popularity relative to both opponents combined. In this case, this metric would make Gray the winner, as Gray has highest average win-loss margin:

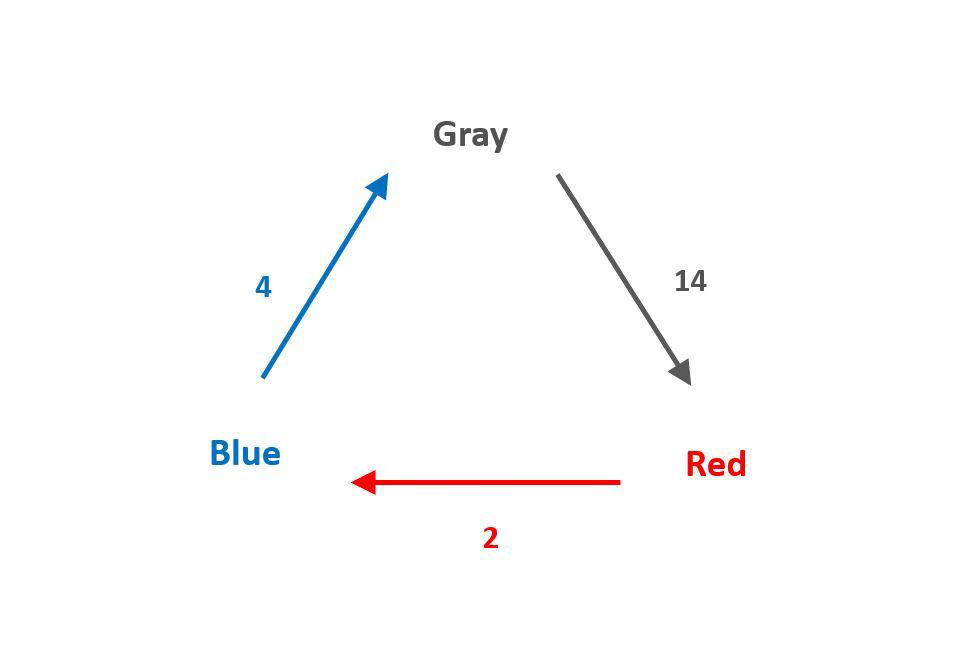
Gray has a 14-point margin of victory over Red and a 4-point margin of defeat against Blue, for a 5-point average: (14-4)/2=5.

Blue has 4-point margin of victory over Gray and a 2-point margin of defeat against Red, for a 1-point average: (4-2)/2=1.

Red has a 2-point margin of victory over Blue and a 14-point margin of defeat against Gray, for a negative-six (-6) point average: (2-14)/2=-6.

Another, even simpler way to decide this election, given the 1-1 tie among all three candidates in terms of their win-loss (W/L) record against each other opponent, is to elect the candidate whose single margin of defeat is the narrowest. This method would put into office the candidate who comes closest to having two head-to-head victories against, and thus being majority-preferred over, each opponent. In this example, Blue wins the election according to this method, as Blue’s single 2-point margin of defeat is the narrowest.

Can the philosophy of democracy tell us which of these two methods is the better way to choose the single officeholder to represent the entire electorate, as in the case of a president?

The first method would be best if the goal is to maximize the preferences of all voters across all options. If the election were to determine where to locate a new public monument, or what the design of that monument should be, the first method would make sense. In that situation, the goal would be to settle upon the result that achieves the highest net favorability among all voters.

But what is the goal when electing a single officeholder, like president or governor, on behalf of the entire electorate? Is it to choose the candidate with the highest net favorability among all voters? Or instead, is it to select the candidate who is acceptable to the most voters given their divergent views on who should be entrusted with the power to make decisions affecting the whole society and its long-term welfare?

If the latter is the goal, then the second method is better. By electing the candidate whose single margin of defeat is the narrowest, this method puts into office the candidate who is acceptable to the broadest coalition of voters. Because this candidate had one victory as well as one defeat, we know that this candidate is acceptable to the majority of voters who preferred that candidate to one of the two opponents. Then, because we know that all three candidates were disfavored by a majority of voters compared to one other candidate, we also know that the candidate with the narrowest margin of defeat is the one whom the fewest voters disfavor. Thus, of the three, this candidate is the one whom the most voters are willing to have put into office compared to each alternative.

Another way to put this basic point is to say that the candidate with the narrowest margin of defeat is the one whom, if in office, the fewest number of voters want to replace with a different candidate. In our hypothetical example, if Red is elected, a large majority—57% to 43%—would prefer to replace Red with Gray. If Gray is elected, a significantly smaller but still decisive majority—52% to 48%—would want to replace Gray with Blue. But if Blue is elected, only the narrowest of majorities—51% to 49%—would want to substitute Red for Blue. From this perspective, one can say that electing Blue is the fairest way of treating all voters as equals because the fewest number of voters are dissatisfied—and thus the largest number of voters are satisfied—with this outcome compared to the alternatives.

Several scholars have developed a way to visualize this point.  It is possible to depict the three-way tie among these candidates, with each having a 1-1 W/L record against their two opponents, as a triangle:

This first triangle shows the percentage of votes each candidate received against each opponent, with the solid arrow showing the direction of dominance (pointing toward the defeated candidate in each head-to-head). From this first triangle, we can create a second that depicts each candidate’s margin of victory:

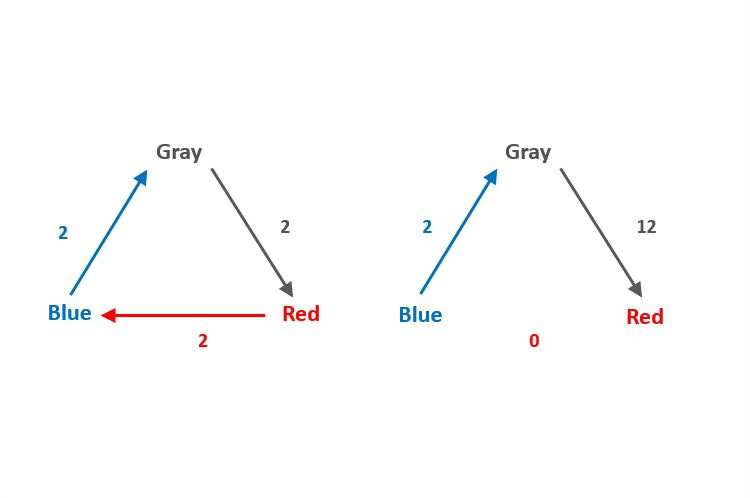
Now we can divide this margin-of-victory triangle into two components:

The first component, on the left, shows the portion of their triangular (or cyclical) relationship in which the three candidates are equivalent: where each candidate has a margin-of-victory of 2 over one other candidate. The left triangle, in other words, depicts the degree to which the three candidates are tied in their superiority to one opponent. The other component, on the right, shows the remaining portion of each candidate’s margin of victory over one opponent. The remaining margins in the right triangle are what’s left over after subtracting the equal 2-point margin from each candidate’s victory.  On the right, Blue’s margin over Gray is now 2 (instead of 4), Gray’s margin over Red is now 12 (instead of 14), and Red’s margin over Blue is now 0 (instead of 2).

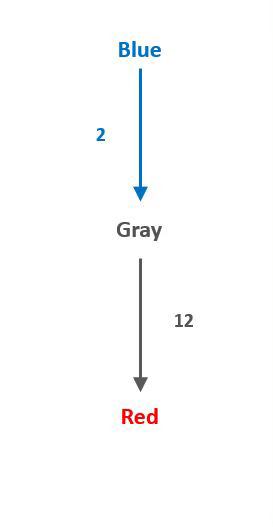
Thus, once the equivalent (or tied) component is removed, we can see that Red no longer has any superiority over an opponent. In this sense, there is no longer a cyclical relationship among the three candidates. Instead, Gray is superior to Red, and Blue is superior to Gray, and Red is superior to no one and thus at the bottom. We can now depict this linear, and not triangular, relationship among the three candidates this way:

This linear relationship shows why Blue should win the election. Because Red’s margin of victory is the smallest, Red is the weakest of the three candidates. Red does not dominate any opponent once the extent to which the candidates are equivalent in relation to each other is set aside. Gray clearly dominates Red, as many more voters prefer Gray to Red (even beyond their degree of equivalence), and Blue dominates Gray, as more voters prefer Blue to Gray (also beyond their degree of equivalence). Thus, Blue is the most dominant candidate and should prevail.

This depiction accords with the fundamental democratic principle that, given their disagreement over which candidate should win, more voters always should prevail over fewer voters. Red’s head-to-head majority over Blue is the smallest—involving the fewest voters—and therefore of the three candidates Red is the one with the least democratic claim to represent the entire electorate. Once Red is eliminated from contention on this basis, Blue beats Gray because a majority of voters favor Blue over Gray.

This set of diagrams helps to understand the second of the two electoral methods for resolving the 1-1 tie among the three candidates in terms of their head-to-head victories. I call this method “Maximum Convergence Voting” because, as the visualization shows, it elects the candidate who has the broadest support within the electorate—the one whom the fewest voters would want to replace with another candidate. The visualization also highlights the reasons for believing that this method is the fairest way to elect a single officeholder to make decisions about what best serves the overall public interest on behalf of all voters, treating them as equals, given that they have divergent views in two dimensions of public policy.

This visualization can’t definitively settle the philosophical question whether Maximum Convergence Voting is a better way to implement democratic values than the first method, which (as we saw) would elect the candidate whose average margin of victory is the highest. That first method has its advocates, including the French mathematician who developed it, Jean-Charles de Borda, and after whom it’s named the Borda count. Much more can and should be said elsewhere about the philosophical choice between these two methods. Here it suffices to make the point that, given the goal of electing a single officeholder to govern on behalf of the entire polity, there is sound philosophical justification for preferring Maximum Convergence Voting because it prioritizes the number of voters who are satisfied with the outcome.

The most important conclusion from the foregoing analysis is that, whichever of the two methods is chosen, there is a coherent way to conduct an election when competition among the candidates exists in two dimensions and leaves the electorate without a candidate whom a majority prefer over each opponent. Despite this division, democracy is still possible in this context. The candidate with the highest net favorability can be elected or, better yet, the candidate who is satisfactory to more voters than any other candidate. Either way, the collective will of the voters can be translated into governance on behalf of the community until it is time for the next election, when the updated collective will of the voters can be determined.