Why Majority-Preferred Candidates Should Win Single-Seat Elections

The first in a series of essays on the philosophy of democracy and its implications.

How to elect a single officeholder to represent an entire country? That’s a question that every country with a presidential rather than purely parliamentary democracy must answer.

It is widely accepted that the goal is to elect a candidate whom a majority of the voters support. For presidential elections in the U.S., most Americans support replacing the Electoral College with a system that would let a majority of Americans nationwide elect the president. Even supporters of the Electoral College recognize that it’s problematic when a candidate who wins a majority of the votes nationwide is not the Electoral College winner.

However, it’s not as easy as one might think to have a system that elects the candidate whom a majority of voters want. Simply electing the candidate with the most votes isn’t enough, because the most votes—a plurality—isn’t necessarily a majority, which must be more than 50%. If there are three or more candidates in contention, then votes might be split among them in such a way that none receives a majority.

Ideally, an electoral procedure would ascertain and put into office the candidate whom a majority of voters prefer to each alternative.  To illustrate this basic truth, let’s imagine an election with three candidates: Blue, Purple, and Red. Suppose 40% of voters would prefer Blue, 35% Red, and 25% Purple. Under the “first-past-the-post” electoral system, which most of America uses, Blue would be elected by having the most votes. 

But we can imagine Red saying something like, “Wait a minute. More voters prefer me to Blue, and therefore I should win.” If put to the test, Red’s claim could very well be true: compared one-on-one against Blue, without Purple in the mix, Red might win more votes. This would be the case if enough of Purple’s supporters favored Red rather than Blue as their second choice. Runoff systems, including instant runoffs with ranked-choice ballots, are able to identify this majority preference for Red over Blue. 

Therefore, one can argue that runoff systems are a better way to elect an officeholder, like a president, who is supposed to represent the entire electorate as democratically as possible. More voters would rather have Red than Blue as president, and so a fairer—more democratic—electoral process, giving equal weight to each voter’s preference, would elect Red instead of Blue. Indeed, France (among other nations) uses a runoff system of this nature precisely for this reason. 

But if we want to be sure to elect the candidate who is truly preferred by a majority of voters, we need to do more than operate this kind of runoff. Suppose that after Red replaces Blue as the declared winner of this three-way race, Purple pipes up: “Wait one more minute! More voters prefer me to Red, and so I should be the one to win!” We can test this claim as well, and it too could easily be true: if enough of Blue’s supporters prefer Purple over Red as their second choice, then a majority of voters would want Purple rather than Red to be elected. 

What is more, a majority of voters might also prefer Purple to Blue. This would be true as long as enough of Red’s supporters would rather have Purple than Blue. In the situation where different overlapping majorities of voters prefer Purple to either Red or Blue, when Purple is paired one-on-one against each other opponent, Purple should be the candidate elected. Of the three choices, Purple is the fairest way to represent the whole electorate, considering all voters democratically as equals: more voters prefer Purple to be their president than Red, and more voters prefer Purple to be their president than Blue. 

For some, this conclusion is difficult to accept given that Purple comes in third in the first-past-the-post system, when voters are asked only which candidate among all in the race is their first choice to win. But whenever there are more than two candidates, first-past-the-post is not a reliable way to identify which candidate is the one most preferred by a majority of voters. The way to do that is suggested by the thought experiment above: to test each candidate against each other opponent, as in a round-robin tournament, to see who wins these direct head-to-head comparisons.  If there is one candidate who beats all others in these, that candidate deserves to win the election. In this situation, that candidate is the one whom a majority of voters prefer over each alternative, and thus this candidate is the one most representative of the entire electorate. 

If we conceive of the electorate as arrayed along a spectrum from the bluest voter on the left to the reddest voter on the right, this procedure of direct head-to-head comparisons will find the candidate closest to the median voter—the one for whom half the voters are to the left and the other half are to the right. It may also help to visualize this blue-red spectrum as divided into gradients, from 0 to 100, much like a football field. In this analogy, pure purple—right in the middle between red and blue—would be at the 50-yard line, while deepest blue and deepest red would be in the opposite endzones.

For sake of simplicity, we can imagine an electorate with a median voter who is perfect purple and thus at the 50-yard line. However, we should note that this need not be the case and in fact is unlikely to be. For example, in another electorate 60% of its voters might be blue, with only 10% purple and 30% red; in this case, the median voter will be among the 60% who are blue—specifically, a blue voter who is closer to purple than five-sixth of the other blue voters and thus perhaps somewhere near the 35-yard line depending on the exact distribution along the spectrum of all voters.

For now let’s assume that the median voter of the relevant electorate is at the 50-yard line. Let’s also assume that one of the candidates in the election is on the blue 40-yard line while another candidate is on the red 30-yard line:

As long as voters prefer the candidate who is closest to them on the blue-red spectrum (whether or not the closest candidate is to the left or the right of them), then the first of these two candidates will prevail when the voters directly compare the pair head-to-head. This is because the candidate at the blue 40-yard line is closer to the median voter (who, again in this example, is at the 50-yard line) than the candidate at the red 30-yard line. Because by definition half the voters in the electorate are to the left of the median voter, and because the candidate at the blue 40-yard line is closer to all the voters left of the median voter than is the candidate at the red 30-yard line—indeed, this half of the electorate is further from the latter (red-side) candidate than the median voter is—it is necessarily true that a majority of voters prefer the former (blue-side) candidate over the latter (red-side) opponent. Thus, as between these two candidates, the former better represents the entirety of the electorate.

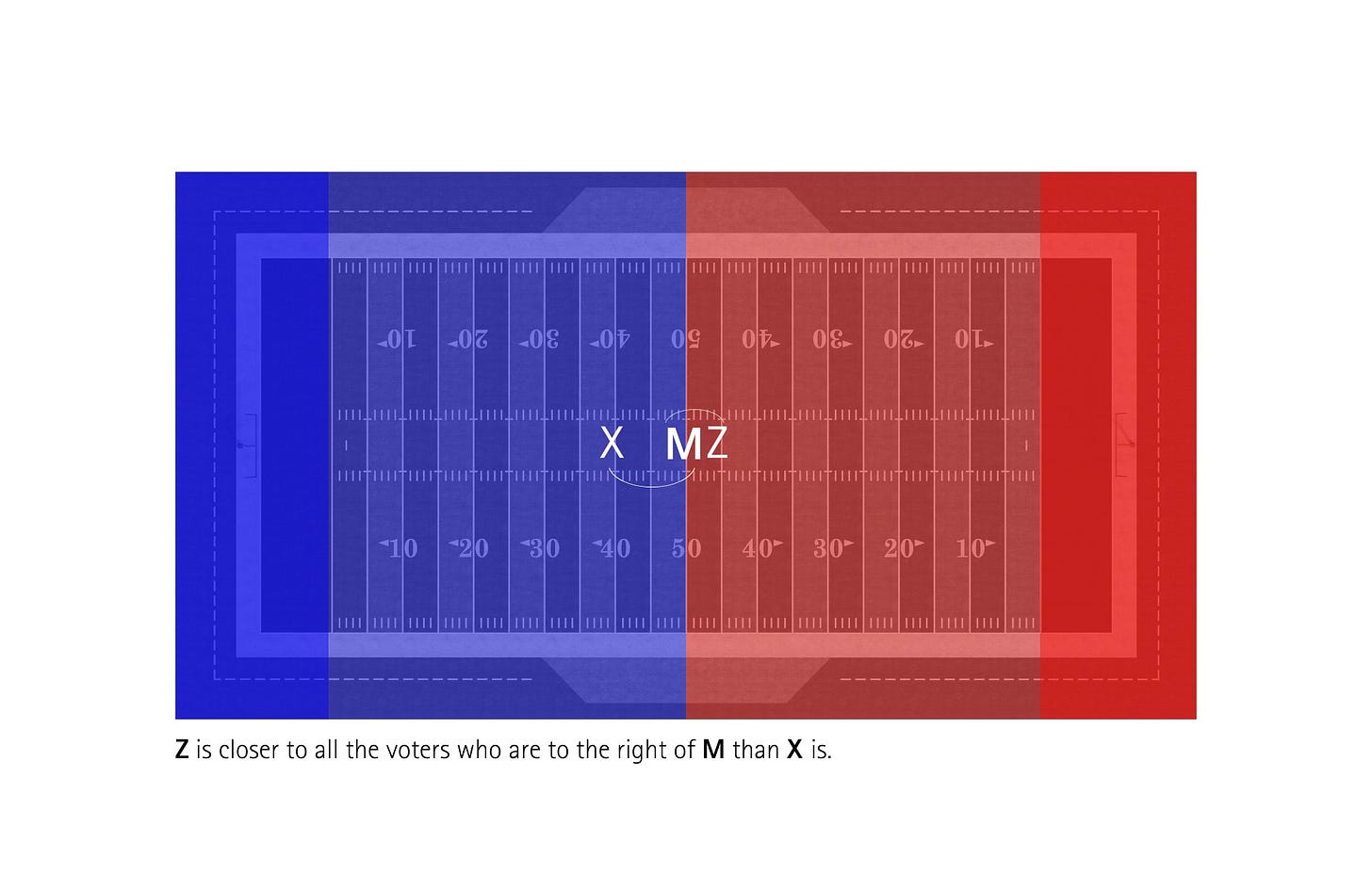
Now suppose there is a third candidate in contention who is at the red 45-yard line:

This third candidate is closer to the median voter (at the 50-yard line) than is the candidate at the blue 40-yard line. Thus, as between these two candidates, a majority of voters prefer the one at the red 45-yard line: the half of the electorate to the right of the median voter all prefer this third candidate over the opponent at the blue 40-yard line. Consequently, this third candidate is the one who (of the three contenders, at least so far) should win the election as the one most representative of all the voters given their preferences.

This process of head-to-head comparisons can (and should) continue if there are other candidates in the race. Any candidate who is even closer to the median voter than the one at the red 45-yard line would become the new most deserving candidate as a result of being favored by a majority of voters over each of the others. It could be a candidate at the 47-yard line, for example, on either the blue or red side. Conversely, any additional candidate further from median voter, perhaps at either 42-yard line, would not be preferred by a majority in comparison to the one (at the red 45-yard line) already identified as most representative of the overall electorate.

Inevitably, the process of direct one-on-one comparisons between each pair of candidates yields the candidate who is closest to the median voter as the one who should win the election. This candidate may be relatively close, or relatively far, from the median voter depending on the strength of the competition. The winning candidate might be at the 49-yard line and thus extremely close to the median voter in this electorate. But if it turns out that there is no candidate closer to the median voter than one at either 40-yard line, then that candidate should prevail even though not especially close. Yet compared to candidates at the 35- or 30-yard lines, or even further away from the median voter, this one is majority-preferred over each alternative and thus most deserving to win this particular election.

I have heard it said, in response to this description of how the process of head-to-head comparisons work, that it is unfair that the candidate closest to the median voter always wins according to this procedure. This system is “biased” in favor of more moderate candidates, according to this criticism. It would be better, the argument goes, to give candidates to the left or the right a chance to win.

This critique is misguided insofar as it doesn’t distinguish between the concepts of the median voter, on the one hand, and political moderation and centrism, on the other. Again, the median voter may or may not be at the center of the political spectrum. If the median voter in a particular electorate is well downfield towards either the blue or red endzone, a perfectly purple candidate at the 50-yard line is unlikely to be the one closest to the median voter and thus unlikely to win the election. Moreover, insofar as voters change their own positions on the political spectrum in response to events and the advocacy undertaken by candidates, voters are open to persuasion and candidates on the left or right can end up winning to the extent that they persuade enough voters.

But perhaps the critique runs deeper and challenges the whole idea of electing the candidate closest to the median voter. If this is indeed the critique, it is mistaken for an even more fundamental reason. What other candidate would be more deserving to be elected than the one closest to the median voter, and why? Assuming for the moment that it is accurate to depict all candidates and all voters as arrayed along the blue-red spectrum, why would it be fairer to elect a candidate who is further from the median voter than an opponent, wherever those particular candidates and the median voter happen to be along that continuum?

It would be nice of course if all voters agreed on which candidate is best for the office. But elections are necessary precisely because voters disagree on who should serve. Given this disagreement, what’s the election procedure that’s fairest to all voters? It is one where a majority of voters prevail, because otherwise fewer voters get their way—and that’s not right if all voters are to be treated equally. So, we are back to the democratic necessity of electing the candidate whom a majority of voters prefer compared to each of the alternatives. This necessity in turn means electing the candidate closest to the median voter, because by definition the median voter is always part of the majority.

Other voters of course will be part of the majority as well. Indeed, when there are multiple candidates, there may be different overlapping majorities that all converge upon the single winner of each head-to-head comparison—hence the name “Convergence Voting” for this kind of head-to-head comparative procedure. But the median voter will always be inside the converging majorities that favor the same candidate over each competitor. Thus, the election’s winner should be the candidate closest to the median voter not because the median voter should be some kind of dictator, or privileged citizen, but simply because identifying the candidate closest to the median voter happens to be the procedure that is fairest to all voters treated democratically as equals.

The next essay in this series will set aside the assumption that all voters and candidates can be located on a single blue-red spectrum and consider the implications of abandoning this assumption for the philosophy of democratic elections.